Odak modu
İstatistik
Ortalama, Varyans ve Standart Sapma
Ortalama, Varyans ve Standart Sapma
Ortalama
Ortalama, bir veri setindeki tüm verilerin (sayıların) toplamının veri sayısına bölümüdür. μ sembolü ile gösterilir. Hesaplanması aşağıda gösterilmiştir:
Örneğin, 5 öğrencinin notları 60, 80, 90, 100 ve 70 ise bu veri setinin, yani öğrencilerin notlarının, ortalaması: <br> (60 + 80 + 90 + 100 + 70) / 5 = 80 olarak bulunur.
Varyans
Varyans, bir veri setindeki tüm verilerin, veri setinin ortalamasına olan uzaklıklarının ortalamasıdır. σ^2 sembolü, yani standart sapmanın karesi, ile gösterilir. Varyans, verilerin ne kadar birbirinden uzak yanı dağılmış olduklarını ölçer. Hesaplanırken önce ortalama bulunur, sonra tüm verilerin ortalama ile olan farklarının kareleri alınarak toplanır ve çıkan sayı toplam veri sayısına bölünür. Hesaplanması aşağıda gösterilmiştir:
Hadi öğrencilerin notlarının varyansını hesaplayalım! Ortalamayı az önce 80 olarak bulduk. Şimdi tüm sayıların ortalama ile olan farklarını hesaplayalım: 60 - 80 = -20, 80 - 80 = 0, 90 - 80 = 10, 100 - 80 = 20 ve 70 - 80 = -10. Farkları -20, 0, 10, 20 ve -10 olarak bulduk, şimdi bu farkların karesini alalım: (-20)^2 = 400, 0^2 = 0, 10^2 = 100, 20^2 = 400 ve (-10)^2 = 100. Farkların karelerini de 400, 0, 100, 400 ve 100 olarak bulduk. Fark edersek farkların karelerini aldığımız zaman sayılar negatif olmaktan çıktı. Bu bize uzaklık bilgisini, yani negatif olamayan bilgiyi sağladı. Bulduğumuz kareleri toplayalım: 400 + 0 + 100 + 400 + 100 = 1000. Bu sayıyı da toplam veri sayısına bölelim: 1000 / 5 = 200. Evet! Bu dağılımın varyansı 200. Eğer öğrencilerin notları 70, 75, 80, 85 ve 90 olsaydı varyans kaç çıkardı? İsterseniz kendiniz hesaplayın, sonra devam edelim. Bu notların varyansını hesapladığımızda sonuç 50 çıkacaktır. Gördüğümüz gibi veriler birbirine daha yakın olduğunda varyans daha az olmakta.
Standart Sapma
Standart sapma, varyansın kareköküdür. Peki neden? Varyansı hesaplarken farkların karesini aldık. Peki karelerini aldıktan sonra karekökünü almak kulağa hoş gelmiyor mu? Farkların karelerini aldıktan sonra karekök alınarak sayı tekrar aynı boyuta döndürülür ve bu işlem de bize yine verilerin birbirinden ne kadar uzak olduğunu gösteren standart sapmayı verir. Hesaplanması aşağıda gösterilmiştir:
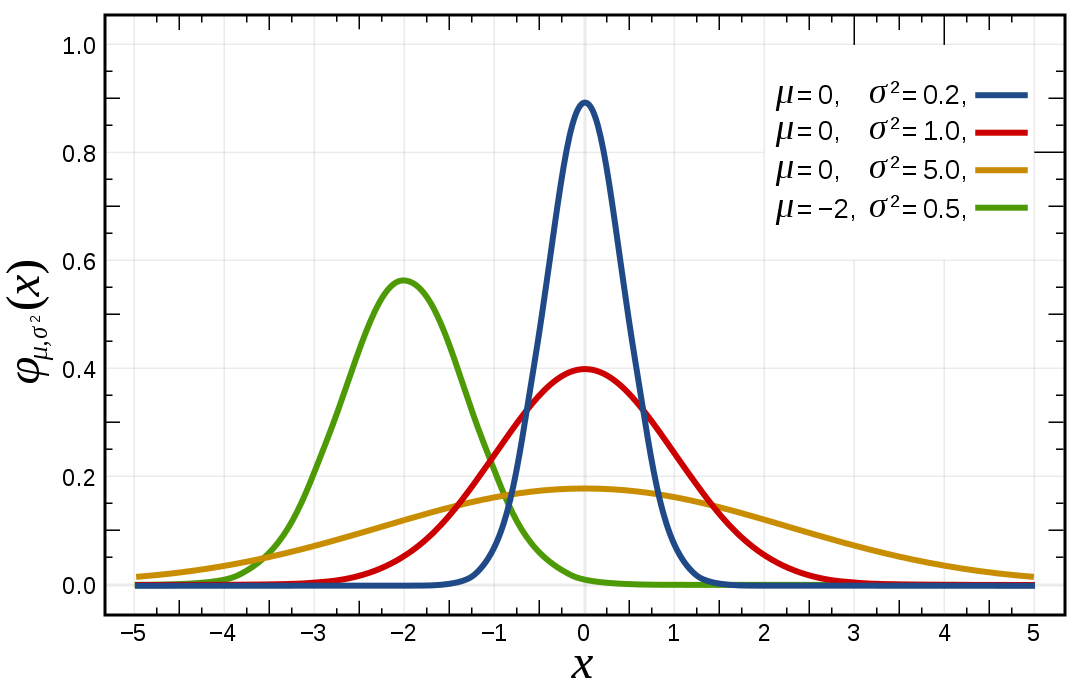
Yukarıdaki grafikte farklı ortalama ve standart sapmalara sahip normal dağılımlar gösterilmekte. Dağılımların ortalama değerleri (μ sembolü ile gösterilmekte) gördüğümüz gibi normal dağılımların merkezleri, yani tepe noktalarıdır. Varyanslarına (σ^2 sembolü ile gösterilmekte) bakacak olursak varyansı fazla olanların daha geniş ve yayılmış olduğunu, varyansı az olanların ise daha dar ve keskin olduğunu görürüz.

Yazılım Kariyerinde İlerlemeni Hızlandıracak Programlar
Patika+ programlarımız ile 4-8 aylık yoğun yazılım kamplarına katıl, temel bilgilerden başlayarak kapsamlı bilgiler edin, yazılım kariyerine başla!

Yorumlar
Yorum yapabilmek için derse kayıt olmalısın!